Естественный интеллект (ЕИ) человека представляет собой уникальное эволюционное
единство
абстрактного, рационально-логического, лево-полушарного (ЛП) мышления и интуитивного, образного, право-полушарного
ПП) мышления. Основной социально-генетической функцией ЕИ, функцией, которая обеспечила беспрецедентный эволюционный
скачок последних двух тысячелетий в развитии человеческой цивилизации, является
порождение нового знания.
Согласно Анри Пуанкаре и Дмитрию Поспелову, определяющую роль в процессе порождения
нового знания играют
мета-процедуры интуитивного, образного ПП-мышления. Однако, еще в начале 80-х годов прошлого века Д.А.Поспелов
отмечал (в книге "Фантазия или реальность") опасный формалистический "ЛП-крен" в разработке систем искусственного
интеллекта (ИИ). Последующее развитие информационных технологий, особенно графических средств представления и
обработки информации, позволило этот "крен" существенно уменьшить. Как бы то ни было, если ИИ желает быть
достойным "преемником" ЕИ человека, он (ИИ) должен научиться ... "мыслить образами" (Эйнштейн).
С точки зрения проблематики ИИ, принято различать два вида компьютерной графики:
иллюстративную компьютерную графику (ИКГ) и
когнитивную компьютерную графику (ККГ). ИКГ визуализирует
уже
известное знание, ККГ визуализирует знание еще
никому не известное посредством создания
цвето-музыкальных ККГ-образов научных абстракций.
В начале 90-х, совместно с Д.А.Поспеловым, нами была разработана концепция
Когнитивной
Реальности, в основе которой лежит мульти-медийная технология
когнитивной компьютерной графики.
На основе этой концепции была создана ККГ-система "ПИФАГОР", которая позволяет человеку погружаться в
цвето-музыкальный мир математических абстракций самого высокого уровня, физически манипулировать этими
абстрактными объектами и
физически общаться с ними в когнитивном 2D-пространстве одновременно
по визуальному, музыкальному, семантическому, эстетическому и даже этическому каналам.
При определенных условиях такие цвето-музыкальные ККГ-изображения (так называемые ПИФОГРАММЫ)
математических абстракций порождают в голове человека новые идеи, которые без ККГ на протяжении тысячелетий
оставались недоступными для исследователей (см.
http://www.ccas.ru/alexzen/).
Цель данной презентации - показать, что "красота есть первый критерий совершенства
математического знания, ибо в мире нет места для некрасивой математики" (Г.Харди), что "логика есть орудие
доказательства; интуиция есть орудие изобретательства" (А.Пуанкаре), что даже самые высоко абстрактные математические
концепции и проблемы могут быть сделаны видимыми, красивыми, привлекательными и понятными даже детям.
Такие динамические ККГ-образы научных абстракций являются эффективным средством активизации интеллектуальной
интуиции и творческого, визуального мышления человека на высших уровнях познания и способствуют рождению
действительно парадигмально-нового знания (сегодня пока) в голове человека.
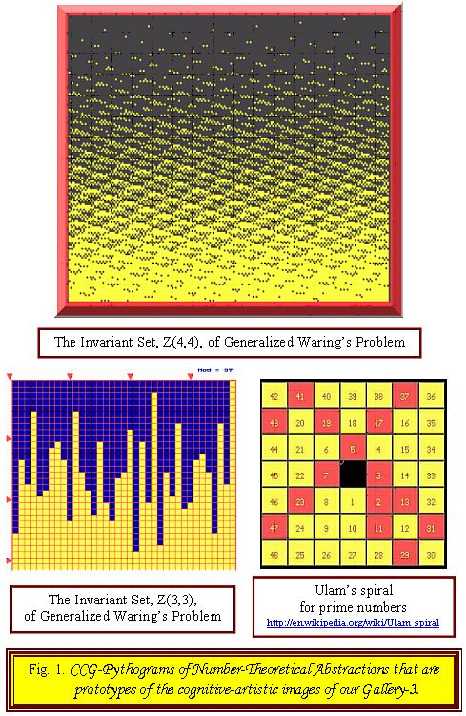
Прототипами всех художественных произведений, представленных в Галерее-3 (см. ниже),
являются ККГ-образы математических
абстракций: распределение простых чисел по спирали Улама, инвариантные множества
Обобщенной Проблемы Варинга, теория времени Велимира Хлебникова, знаменитая проблема континуума, ККГ-образы чисел
, е, 2 и т.д. (см. Рис 1 и 2). Это значит, что семантическим и онтологическим контекстом художественных образов
являются имманентные, абсолютные, вечные числовые структуры, родственные по своей космической эзотерике "звездному
небу над головой и моральному Закону в нашей душе" (И.Кант). Именно с этой точки зрения следует воспринимать
интеллектуальную эстетику представленных картин.
Еще несколько слов о ближайших перспективах восстановления (сегодня почти утраченного)
леонардовского Единства "левого и правого". Глобальная сеть, подобная Internet, в полном объеме впитавшая в себя
новейшие достижения микро-, опто-, нано-, крио- и тому подобной электроники и технологии Виртуальной Реальности,
очень в недалеком будущем превратится в наиболее естественную
среду обитания совокупного интеллекта мирового
научно-художественного сообщества, а системы Когнитивной Реальности - в принципиально новую технологию глобального
высоко-нравственно-разумно-эстетического постижения Мира, включая в него, а не традиционно ему противопоставляя,
Человека... А, возможно, со временем - и в новую высшую форму распределенного существования Субстанции Разумной.
Следует еще раз подчеркнуть, что именно искусственный интеллект "в лице" технологии
Когнитивной Реальности позволяет уже сегодня реализовать идущую от Пифагора идею о высшей гармонии Числа и Музыки,
Науки и Искусства, ККГ-Обpаза и Мысли, Пребывающего во Времени и вне Его ...
ВМЕСТО ХУДОЖЕСТВЕННОЙ БИБЛИОГРАФИИ.
Данная Выставка является продолжением серии выставок "Математика и Искусство", проводившихся
в рамках различных Российских и Международных научных конференций по математике, информатике и искусственному
интеллекту. Вот краткий перечень некоторых из этих выставок.
Выставка "Когнитивная эстетика математических абстракций". - Государственный литературный
музей, май, 2005.
Выставка "Математика и искусство" в рамках Всесоюзной конференции "Научная сессия МИФИ-2004".
Alexander Zenkin, Anton Zenkin, Cognitive-Aesthetic Images Of Mathematical Abstractions. -
Artworks For "Ars (Dis)Symmetrica'03" Exhibition. CD-Proceedings of the SYMMETRY FESTIVAL-2003 where Science
Meets Art, 18-24 August, 2003,
http://www.conferences.hu/symmetry2003/festival-Pre.html
http://www.ccas.ru/alexzen/gallery2/Gallery-2.htm
Выставка "Когнитивная визуализация - Математика - Искусство". - Съезд Российской Ассоциации
Искусственного Интеллекта. Институт Проблем Управления РАН, 19 ноября, 2003.
http://www.ccas.ru/alexzen/gallery2/Gallery-2.htm
Выставка "Математика и искусство" в рамках Первой Международной Конференции
"p-Адическая Математическая Физика", Математический институт им. Стеклова РАН, октябрь, 2003 г.
Presentation "Intellectual Aesthetics of Mathematical Abstractions.
The Unity of the Left-Hemispheric, Rational, Abstract Thinking and the Right-Hemispheric, Intuitive, Visual One". -
The 5th International Congress & Exhibition of the International Society for the Interdisciplinary Study of Symmetry.
Sydney, 8-14 July, 2001. Intersections of Art and Science. See at:
http://www.isis-s.unsw.edu.au/interact/gallery/image_files/zenkin/a_zenkin.html
Выставка "Когнитивная реальность - новая технология научного познания". -
ФОКОМ & ПОЛИТЕХНИЧЕСКИЙ МУЗЕЙ, Выставка и научные чтения "Компьютер: на пороге Тысячелетий". Декабрь 13, 2000.
Alexander A.Zenkin, Anton A.Zenkin, Presentation of the CCG-Technology in George Washington
University, Washington, March, 2000. - Опубликован буклет (и его интернет-версия) с содержанием лекции (30 стр.).
ИСТОРИЯ ПРОБЛЕМЫ НА ЯЗЫКЕ ССЫЛОК
Все началось с фантастически смелого решения Д.А.Поспелова опубликовать в журнале
"Новости Искусственного Интеллекта" следующие статьи А.А.Зенкина.
А.А.Зенкин,
Знание-порождающие технологии когнитивной реальности. -
Новости Искусственного Интеллекта, 1996, No. 2, стр. 72-78.
А.А.Зенкин,
"О Логике Некоторых Квази-Финитных Рассуждений Теории Множеств и Метаматематики.
Новый Парадокс Канторовской Теории Множеств." - Новости искусственного интеллекта, 1997, No. 1, pp. 64-98.
А.А.Зенкин,
Существует ли Г.Бог в Трансфинитном Раю Г.Кантора? -
Новости искусственного интеллекта, 1997, No. 1, стр. 156-160.
А.А.Зенкин,
Автоматическая классификация парадоксов логики и математики.
Об одной "физической" модели парадокса "лжеца". - Новости искусственного интеллекта, 1997, No. 3, стр. 69-79.
А.А.Зенкин,
Трансфинитная кавитация в рядах ординалов Г.Кантора. -
Новости искусственного интеллекта, 1997, No. 3, стр. 131-137.
Д.А.Поспелов оказался провидцем и в этом разделе современной науки: ККГ-визуализация
математических абстракций помогла нам увидеть целый ряд фатальных дефектов в области современной символической
логики, мета-математики и аксиоматической теории множеств (АТМ).
Выдающиеся канторианцы (термин Пуанкаре) Френкель и Бар-Хиллел (см. Основания теории множеств.
- Москва, "МИР", 1966, стр. 244) пишут по этому поводу:
Число ученых, отвергавших концепцию актуальной бесконечности (АБ) и основанную на этой
концепции теорию множеств Г.Кантора, - равно как и современную АТМ, - "было всегда невелико. Удивительнее всего то,
что находясь в относительной изоляции, они высказывали полнейшую убежденность в окончательной победе занимаемой ими
позиции"
В этом заявлении Френкеля и Бар-Хиллела, выражающем сокровенное мнение подавляющего
большинства современных канторианцев, содержатся две неточности. Во-первых, под "относительной изоляцией"
следует понимать не форму "наказания" со стороны "продвинутого большинства" научного сообщества, а тот факт,
что эти ученые, которые
на протяжении тысячелетий отвергали концепцию актуальной бесконечности, жили в
существенно разное время и потому, по определению, не могли участвовать в сговоре (или во взаимном зомбировании)
по поводу неприятия этой АБ-концепции и любых ментальных "конструкций", на ней основанных: эти ученые отвергали АБ потому,
что считали, - и не без основания, - концепцию АБ
внутренне противоречивой. Во-вторых, "число ученых, которые
на
протяжении тысячелетий отвергали АБ-концепцию и любые ментальные "конструкции", на ней основанные", было не так
уж и мало, о чем свидетельствует следующий, далеко не полный список.
СПИСОК-1. ПРОТИВНИКИ АБ "ВСЕХ ВРЕМЕН И НАРОДОВ":
Аристотель, Евклид, Фома Аквинский, Лейбниц, Беркли, Локк, Декарт,
Кант, Спиноза, Лагранж, Гаусс, Кронекер, Лобачевский, Коши, Ф.Клейн, Эрмит, Пуанкаре, Бэр, Борель,
Лебег, Брауэр, Куайн, Виттгенштейн, Вейль, Лузин, и
уже в наши дни - Эррет Бишоп, Соломон Феферман,
Ярослав Перегрин, Владимир Турчин, Петр Вопенка и многие другие выдающиеся
творцы классической логики
и классической математики.
Следует подчеркнуть, что начиная с Кронекера, т.е. примерно с 70-х г.г. XIX века,
протест против использования понятия АБ в математике
как понятия внутренне противоречивого принял форму
резко негативного отношения к теории множеств Георга Кантора,
основанной на алгоритмическом использовании
концепции АБ. Тот же протест и на том же основании относится и к основаниям современной АТМ.
Представляется весьма сомнительным намерение канторианцев, буде таковое реализовано,
противопоставить этому Списку-1 достаточно весомый Список-2 сторонников
современной АТМ, основанной на
АБ-концепции. Конечно, при условии, что аргумент типа "я на две тысячи лет "умнее" Аристотеля" не является
достаточным основанием для "прохождения в члены" Списка-2.
Как бы то ни было, Список-1 на полном для того основании следует пополнить,
по крайней мере, еще двумя действительными членами: Д.А.Поспеловым и А.А.Зенкиным.
КОГНИТИВНАЯ КАРТА НЕКОТОРЫХ ПОСЛЕДНИХ ДОСТИЖЕНИЙ
НА ФРОНТАХ БОРЬБЫ С АТМ-БУРБАКИЗАЦИЕЙ МАТЕМАТИКИ И МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ.
A.A.Zenkin,
Logic of Actual Infinity and G.Cantor's Diagonal Proof of the
Uncountability of the Continuum. - The Review of Modern Logic, Vol. 9, Number 3&4, 27-82 (2004).
A.A.Zenkin,
Scientific Intuition of Genii Against Mytho-'Logic' of Cantor's
Transfinite 'Paradise'. - Philosophia Scientia, 9 (2), 145 - 163 (2005). Published by LPHS - Archives H. Poincar?.
А.Пуанкаре
О науке. - М., 1983.
В.И.Арнольд,
Антинаучная революция и математика. - Вестник РАН, 1999, № 6, 553-558.
А.А.Зенкин,
"Научная контр-революция в математике". - Независимая газета от 19 Июля,
2000 г. Приложение "НГ-НАУКА", стр. 13.
http://science.ng.ru/magnum/2000-07-19/5_mathem.html,
http://www.ccas.ru/alexzen/papers/PAPER2E-01.htm
Ю.Н.Афанасьев,
Может ли образование быть негуманитарным? -
Вопросы философии, 2000, №7, C.37-42.
Solomon Feferman.
In the Light of Logic. - Oxford University Press, 1998,
(Logic and Computation in Philosophy series). See the chapter "Infinity in mathematics: Is Cantor necessary?"
А.А. Зенкин,
Знание-порождающие интеллектуальные системы, основанные на
когнитивной компьютерной графике: логика, интуиция и эстетика научного познания. - Всероссийская
междисциплинарная конференция "Философия искусственного интеллекта", г. Москва, МИЭМ, 17 - 19 января 2005 года,
Секция 5. Интеллектуальные системы в гуманитарных науках. Труды конференции. - М.: ИФ РАН, стр. 351-352.
А.А.Зенкин,
Трансфинитный рай Георга Кантора: библейские сюжеты на пороге апокалипсиса. -
Новости Российской ассоциации искусственного интеллекта,
http://www.raai.org/about/persons/zenkin/pages/tranrai.doc
А.А.Зенкин,
Априорные логические суждения с нулевой онтологией. - Сборник "Математика и опыт",
изд. МГУ, 2004, ред. проф. А.Г.Барабашев, стр. 423-434.
А.А.Зенкин,
Когнитивная визуализация некоторых трансфинитных объектов классической
(канторовской) теории множеств. - В сб. "Бесконечность в математике: философские и исторические аспекты",
ред. проф. А.Г.Барабашев. - М.: "Янус-К", 1997 г., стр. 77-91, 92-96, 184-189, 221-224.
А.А.Зенкин,
"Infinitum Actu Non Datur". - Вопросы философии, 2001, No. 9, 157-169.
http://www.philosophy.ru/library/math/cantor.htm
А.А.Зенкин, "Ошибка Георга Кантора". - Вопросы философии, 2000, No. 2, 165-168.
http://www.ccas.ru/alexzen/papers/Cantor/Fatal_Mistake_of_Cantor.html
http://www.ccas.ru/alexzen/papers/vf1/vf-rus.html
http://www. ccas.ru/alexzen/papers/vf1/vf-eng.html
Выражая единодушное мнение выдающихся членов Списка-1, я "высказываю полнейшую убежденность в окончательной победе занимаемой нами позиции".
"Нас <пока> мало, но наше дело правое. Победа будет за нами!"
INFINITUM ACTU NON DATUR (Aristotle).
ПРИЛОЖЕНИЕ.
GALLERY-3
«ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ:
МАТЕМАТИКА И ИСКУССТВО»



Это не шина прокололась, это не обод сломался ...
Это внутри-системный тектонический разлом цивилизации-XXI ...

















